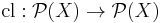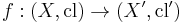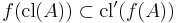Kuratowski closure axioms
In topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition. They were first introduced by Kazimierz Kuratowski, in a slightly different form that applied only to Hausdorff spaces.
A similar set of axioms can be used to define a topological structure using only the dual notion of interior operator.
Contents |
Definition
A topological space 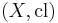 is a set
is a set  with a function
with a function
called the closure operator where 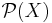 is the power set of
is the power set of  .
.
The closure operator has to satisfy the following properties for all 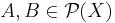
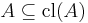 (Extensivity)
(Extensivity)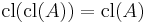 (Idempotence)
(Idempotence)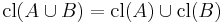 (Preservation of binary unions)
(Preservation of binary unions)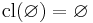 (Preservation of nullary unions)
(Preservation of nullary unions)
If the second axiom, that of idempotence, is relaxed, then the axioms define a preclosure operator.
Notes
By induction, Axioms (3) and (4) are equivalent to the single statement
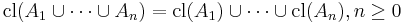 (Preservation of finitary unions).
(Preservation of finitary unions).
Recovering topological definitions
A function between two topological spaces
is called continuous if for all subsets  of
of 
A point  is called close to
is called close to  in
in 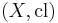 if
if 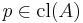
 is called closed in
is called closed in 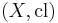 if
if 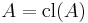 . In other words the closed sets of
. In other words the closed sets of  are the fixed points of the closure operator.
are the fixed points of the closure operator.
If one takes an "open set" to be a set whose complement is closed, then the family of all open sets forms a topology. Conversely, any topology can be induced in this way by the correct choice of closure operator.